Spanning tree in hindi
spanning tree एक graph के द्वारा निर्मित किया जाता है। अर्थात spanning tree एक graph का subset होता है.
एक spanning tree के सभी vertices होंगे और कुछ edges होंगे। मतलब एक spanning tree निर्मित करने के लिए एक graph में जितने भी vertices होंगे। उन सभी vertices का उपयोग करेंगे पर graph के सभी edges में से कुछ ही edge का उपयोग करेंगे।
graph जो है वह cycle के रूप में नहीं होना चाइये। एक spanning tree कभी भी cycle निर्मित नहीं करता है। तथा यह disconnected भी नहीं होना चाहिए.
तो हम कह सकते है कि प्रत्येक connected तथा undirected Graph का कम से कम एक spanning tree होता है.
properties of spanning tree in hindi:-
1:- connected graph की एक से ज्यादा spanning tree हो सकती है.
2:- spanning tree में cycle नही होती है.
3:- अगर हम spanning tree में से एक edge को हटा देंगे तो graph disconnected हो जायेगा.
4:- अगर हम spanning tree में एक edge को add कर देंगे तो वह loop या circuit बना लेगा.
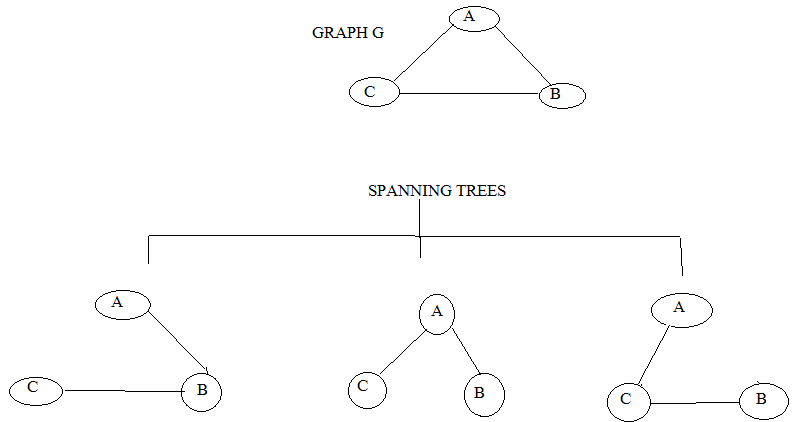
एक graph से कई तरह से spanning tree निर्मित कर सकते है। यहाँ ऊपर एक चित्र में एक graph से तीन तरह के spanning tree बनाया गया है। जिसमे graph के सभी vertices है और कुछ edges है। ध्यान रहे की कोई भी spanning tree एक cycle ना create करे।
Cost of spanning tree :-
एक spanning tree का cost उसके vertices के weights को जोड़ कर निकाल सकते है।
जैसे :-
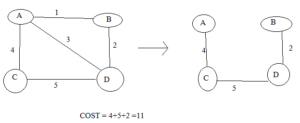
Minimum spanning tree in hindi
Minimum spanning tree एक spanning tree ही होता है। वह spanning tree जिसका cost सबसे कम होता है वह minimum spanning tree कहलाता है।
जैसे :- यहाँ एक graph से spanning tree बनाया गया है जिनके vertices को जोड़ने से सबसे कम cost निकलता है।
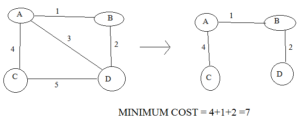
यहाँ minimum spanning tree को find करने के लिए दो प्रकार के algorithm है –
1:- Prim’s algorithm
2:- Kruskal’s algorithm
ये दोनों greedy algorithms है.
Prim’s algorithm in hindi
prim’s algorithm एक greedy algorithm है जिसके द्वारा एक minimum spanning tree find करते है। मतलब एक tree जिसमे सभी edges शामिल होंगे उसके edges का एक subset find करेंगे। prim’s algorithm shortest first path के साथ समानता share करता है।
यह algorithm एक single tree को nodes के जैसे treat करता है और दिए गए graph से spanning tree बनाने के लिए उस पर new node जोड़ता है।
Prim’s algorithm में minimum spanning tree निर्मित करने के लिए सबसे पहले एक vertex से शुरू करेंगे यह कोई भी arbitrary vertex हो सकता है हम कही से भी spanning tree निर्मित करना शुरू कर सकते है। एक vertex को choose करने के बाद उस vertex से जुड़े हुए सभी vertex को देखेंगे कि कौन से vertex का cost सबसे कम है। जिस vertex का cost सबसे कम होगा उस vertex को choose करेंगे और पहले वाले vertex के साथ जोड़ देंगे। यह प्रकिया तब तक चलते रहेगी जब तक सारे vertex ना जुड़ जाये और उसके साथ साथ यह भी ध्यान में रखेंगे कि एक भी cycle ना निर्मित हो।
Algorithm :-
1:- Remove all the loops and all the parallel edges.
( सभी loops और parallel edges को अलग कर देंगे )2:- Choose any arbitrary node as root node.
( एक node को root node के रूप में चुनेंगे यह node कोई सा भी हो सकता है हम कही से भी spanning tree बनाना शुरू कर सकते है। )3:- Check outgoing edges and select the one with less cost.
( Outgoing edges को check करेंगे और उन edges में से एक edge को select करेंगे जिसका cost सबसे कम होगा। )
Ex :-
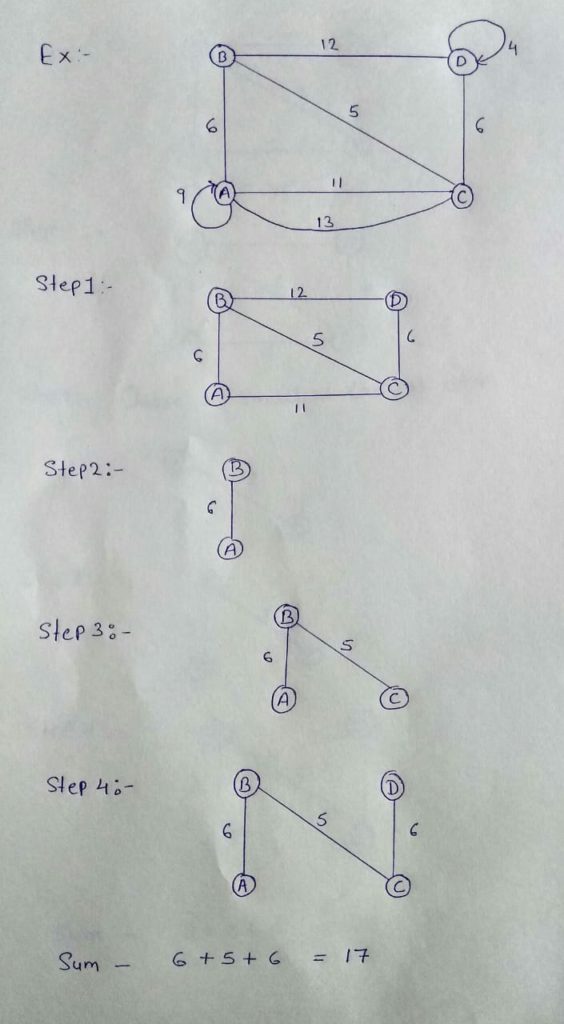
Kruskal’s algorithm in hindi
kruskal’s algorithm एक greedy approach का उपयोग करके minimum spanning tree को find करता है। यह minimum spanning tree को सभी properties को follow करता है।
इस algorithm में graph को एक forest की तरह और सभी nodes को एक individual tree की तरह treat किया जाता है।
Kruskal algorithm की मदद से minimum spanning tree find करने के लिए सबसे पहले एक सबसे कम cost वाला edge choose करेंगे उसके बाद फिर से सबसे कम cost वाला edge choose करेंगे यह प्रक्रिया तब तक चलती रहेगी जब तक की सभी vertex ना जुड़ जाये और साथ साथ एक cycle भी ना निर्मित हो। इसमें हमेशा सबसे कम cost वाला ही edge choose करेंगे फिर चाहे एक vertex दुसरे vertex से ना जुड़े।
Algorithm :-
1:- Remove all the loops and all parallel edges.
( सभी loops और parallel edges को अलग कर देंगे )
2:- Arrange all edges in their increasing order of weight.
( सभी edges को उनके बढ़ते क्रम के weight में arrange करेंगे। )
3:- Add all edges which has the least weightage.
( सभी edges को जोड़ेंगे जिनका महत्त्व या cost सबसे कम है। )
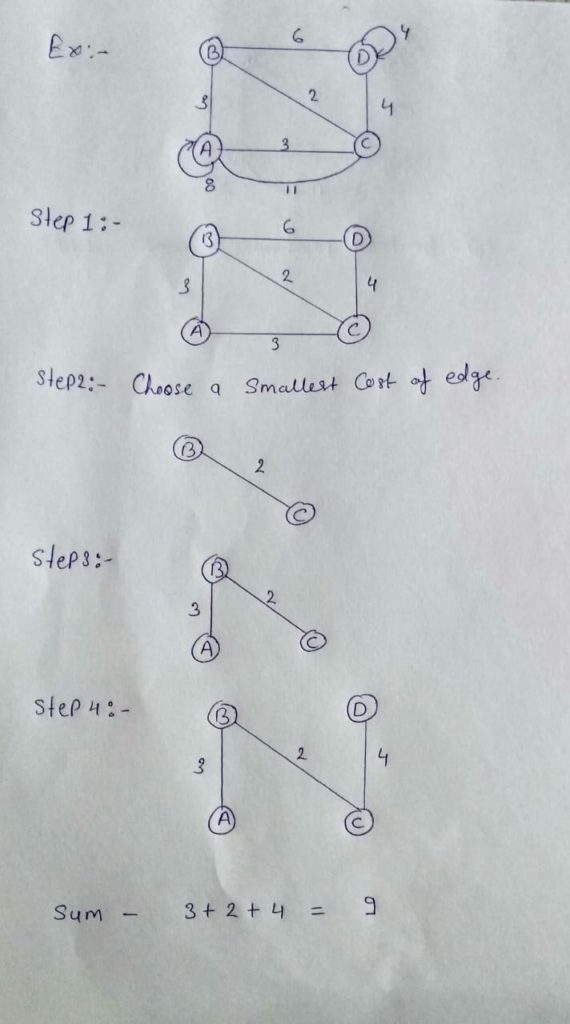
उदाहरण:-
Sir kya aap computer ️ arctectur k baare me jankari de sakte ho