hello friends! आज मैं आपको इस पोस्ट में what is k-map in hindi (के-मैप क्या है?) के बारें में विस्तार से बताऊंगा. तो चलिए start करते हैं:-
K-MAP in Hindi
k-map का पूरा नाम karnaugh मैप है. यह बूलियन व्ज्यंजकों को हल करने की ग्राफीय विधि है. k मैप की सहायता से हम 3, 4 चरों वाले बूलियन व्यंजकों को किसी बूलियन व्यंजकों की प्रमेय के बिना सरल कर सकते हैं.
इसमें SOP (sum of product) और POS (product of sum) तथा सत्य तालिका (truth table) से प्राप्त सूचनाओं को प्रदर्शित किया जाता है.
k मैप को एक तालिका जैसे प्रदर्शित किया जाता है पर यह सत्य तालिका से ज्यादा सुचना प्रदान करता है.
k-map and numbering of cells
k-map में कोष्ठकों (cells) की संख्या इस बात पर निर्भर करती है कि चर राशियों (variable) की संख्या कितनी है. यदि चर राशियाँ n हैं तो कोष्ठकों की संख्या 2n होगी. कोष्ठकों की numbering के लिए grey code का उपयोग किया जाता है. कोष्ठकों को चिन्हित करने के लिए कोष्ठकों को डेसीमल संख्या दी जाती है जो कोष्ठक के ऊपरी बाएं कोने पर दर्शाई जाती है.
दो चर राशि वाला k मैप और उसके कोष्ठकों की numbering-
इसमें कोष्ठकों की संख्या 22=4 होती है. माना कि दो चर राशियाँ A और B हैं, A और B के संयोजन करने पर प्राप्त AB(11) को कोष्ठक 3 प्रदर्शित करता है. AB̅(10) को कोष्ठक 2 प्रदर्शित करता है. A̅B(01) को कोष्ठक 1 और A̅B̅(00) को कोष्ठक 0 प्रदर्शित करता है. नीचे इसका चित्र दिया है:-
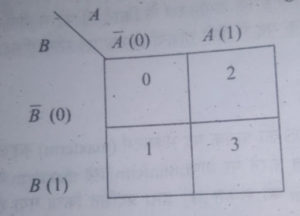
तीन चर राशियों वाला k मैप और उसके कोष्ठकों की numbering–
इसमें कोष्ठकों की संख्या 23=8 होती है. इसमें चर राशि A,B और C संयोजन को प्रदर्शित किया जाता है. चर राशि के संयोजन A̅B̅C̅ (000) को कोष्ठक 0 प्रदर्शित करता है. इसी प्रकार अन्य संयोजनों को उनके डेसीमल संख्या के अनुसार प्रदर्शित किया जाता है.
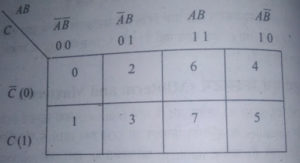
चार चर राशियों वाला k मैप और उसके कोष्ठकों की numbering-
इसमें कोष्ठकों की संख्या 24=16 होती है. इसमें चार चर राशियों (A,B,C,D) के संयोजनों को प्रदर्शित किया जाता है. संयोजनों के डेसीमल तुल्यांक के आधार पर कोष्ठकों को चिन्हित किया जाता है.
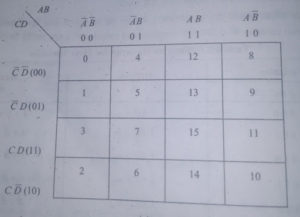
k मैप बनाने में maxterm या minterm में से किसी का भी उपयोग किया जा सकता है. minterm को mi से तथा maxterm को Mi से प्रदर्शित किया जाता है.
जहाँ जहाँ पर ‘1’ होता है उन्हें हमें आयताकार समूह में रखना होता है. समूह में रखने के लिए ‘1’s को पास रहना बहुत जरुरी है तभी हम 1’s बिट का आयताकार समूह बना पाएंगे और आयताकार समूह में 2 की घात के रूप में ही बिट रह सकती हैं. जैसे- 2,4,8. तो इस प्रकार हमें pair, quads और octets प्राप्त होते हैं.
pair- इसमें दो 1’s बिट को आयताकार समूह में लिया जाता है. जो 1’s बिट क्षैतिज या उर्ध्वाधर रूप से एक दुसरे के समीप होती हैं उन बिट्स को इसमें लिया जाता है. इसे सरल करने में एक चर राशि और उसका कॉम्प्लीमेंट (complement) विलुप्त हो जाता है. k मैप में एक अधिक pair हो सकते हैं. इन्हें हल करने के लिए प्रत्येक pair की सरलीकृत समीकरण को “OR” (add) करके बूलियन समीकरण प्राप्त की जाती है.
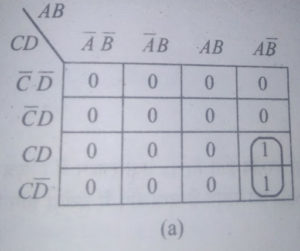
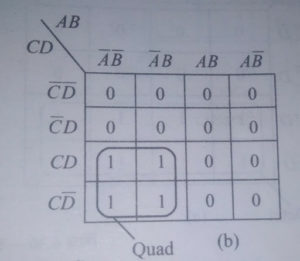
quad- क्वाड में चार 1’s का आयताकार समूह होता है. यह एक line में या एक वर्ग के रूप में एक दुसरे के समीप हो सकते हैं. इसे सरल करने में दो चर राशियाँ और उनके कॉम्प्लीमेंट विलुप्त हो जाती हैं.
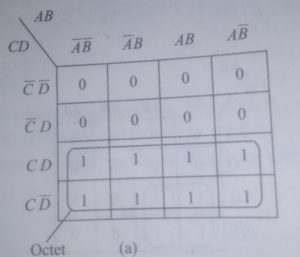
octet- octet आठ 1’s बिट्स का समूह होता है. octet को सरल करने में तीन चर राशियाँ तथा उनके कॉम्प्लीमेंट विलुप्त हो जाते हैं. इसे दो क्वाड के रूप में भी सरल किया जा सकता है.
overlapping groups
k-map में किसी 1’s बिट का उपयोग pair,quad या octet बनाने के लिए एक से ज्यादा बार हो सकता है. मतलब ये कि एक 1’s बिट का उपयोग किसी pair में भी किया जा सकता है और किसी quad या octet में भी किया जा सकता है. इस प्रकार जो समूह बनते हैं उन समूहों को ओवरलैपिंग समूह कहते हैं.
map rolling
k-map में ऐसे भी समूह बनते हैं जिन्हें मैप rolling द्वारा बनाया जाता है. माना एक 1’s बिट मैप के बिलकुल दांयी तरफ है और उसी लाइन में एक 1’s बिट बिलकुल बांयी तरफ है. तब इन दोनों का एक pair बनाने के लिए मैप rolling कर के दांयी तरफ को बांयी से मिलाया जाता है इससे दोनों 1’s का pair बन जाता है. इसी का उपयोग कर quad भी बनाया जा सकता है.
K-map से समीकरण हल करने के चरण
1). चरों की संख्या के अनुसार k मैप का चयन किया जातां है.
2). दी गयी समस्या में से minterm(SOP) या maxterm(POS) को पहचाना जाता है.
3). SOP के लिए मैप के कोष्ठकों में 1 लिखा जाता है और बाकी जगह 0 लिखा जाता है.
4). POS के लिए मैप के कोष्टकों में 0 लिखा जाता है और बाकी जगह 1 लिखा जाता है.
5). अब जहाँ जहाँ पर 1 है उनको आयताकार समूह में 2 की घात(2,4,8) के रूप में रखा जाता है. इसमें जितने हो सकें उतने 1’s को समूह में रखा जाता है. समूह में होने के लिए बिट्स का अगल बगल में होना बहुत जरूरी होता है.
6). अब जो समूह बनते हैं उनमें से product terms को लेकर और फिर उनको जोड़ कर k मैप की सरलीकृत बूलियन समीकरण बनाई जाती है.
NOTE:- अगर आपके लिए यह आर्टिकल helpful रहा हो तो इसे अपने दोस्तों के साथ अवश्य share कीजिये और आपके k-map को लेकर कोई questions हो तो उन्हें comment में बता सकते है. thanks.
Sir, can you tell DE ‘s ke important question??
Map simplification
Product-of-sums simplification
Din’t-Care Conditions
Combinational Circuits
Half-Adder
Full-Adder